命题逻辑(详解)
命题逻辑是种最初目的是为了模型推理的代数,其历史要追溯到亚里士多德的时代。
在更近的时代里,它主要用来计算机电路设计、编程语言和系统(比如Prolog语言)的数据模型。
1 什么是命题逻辑
命题逻辑是让可以对逻辑表达式的真假进行推理的数学模型。简单来说就是通过逻辑推导来判断真假。
1.1 基本的逻辑运算符
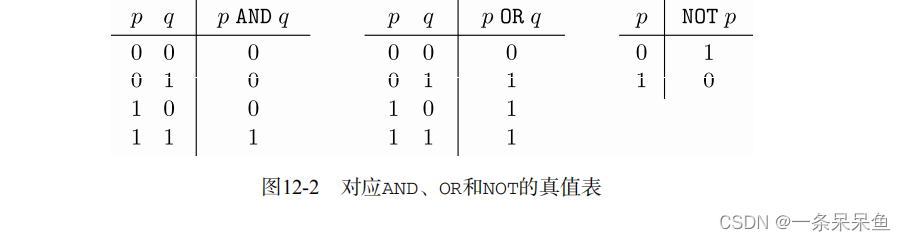
与 AND全真为真或 OR全假为假非(否定) NOT取反
1.2 命题逻辑的缺点
命题逻辑是一种实用的推理工具,但它是有局限性的,因为它不能洞悉命题内部并利用命题间的关系。
if(a<b && b<c && a<c) (1.1)
if(a<b && b<c) (1.2)
很明显 ( 1.1 ) ≡ ( 1.2 ) (1.1) \equiv (1.2) (1.1)≡(1.2)
根据条件设命题
- 命题q : a < b
- 命题p : b < c
- 命题r :a < c
所以
(q AND p AND r AND) ≡ \equiv ≡ (q AND r) (1.3)
但 (1.3) 并不是总成立,当命题q,r为真时,(1.3)左边不成立,右边成立。这是由于命题逻辑无法通过q,r为真来推出 p 命题也为真。
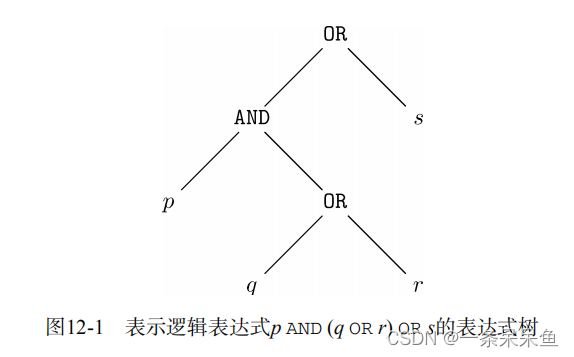
2 逻辑表达式
逻辑表达式是通过命题和逻辑运算符,把某个事件的逻辑表达出来的符号运算式。
2.1 逻辑运算符优先级
NOT > AND > OR
2.1.1其他逻辑运算符
- 蕴含(implication),写为→。p → q的含义是,“如果p为真,那么q为真。

- 等价(equivalence), 写为 ≡ \equiv ≡ ,意思是它表明左边和右边的操作数具有相同的真值。
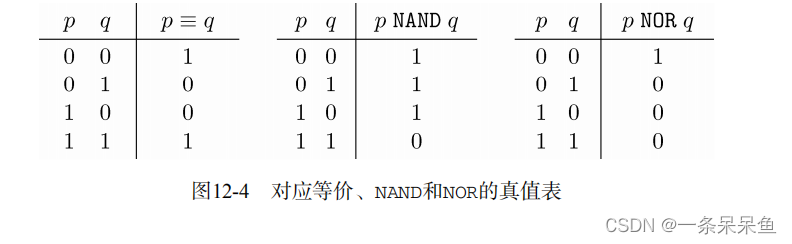
- 与非(NAND) , 是首先对操作数应用AND,然后对得到的结果
应用NOT运算符求补。p NAND q就表示NOT (p AND q)。- 或非(NOR) , 是先对操作数取OR,然后对得到的结果
求补,p NOR q就表示NOT (p OR q)。
NOT > NAND > NOR > AND > OR > ⟶ \longrightarrow ⟶ > ≡ \equiv ≡
2.2 逻辑运算符简写
q A N D p ≡ q p q O R p ≡ q + p N O T q ≡ q ‾ q \enspace AND \enspace p \quad \equiv \quad qp \\ q \enspace OR \enspace p \quad \equiv \quad q + p \\ NOT \enspace q \quad \equiv \quad \overline{q} qANDp≡qpqORp≡q+pNOTq≡q
使用这种新表示法的一个重要原因在于,这样可以让我们把AND和OR视作算术运算中的乘法和加法。因此可以应用诸如交换律、结合律和分配律这样的类似法则。
因为有了这种简化符号,通常可以把表达式的AND称为积,把表达式的OR称为和。表达式的AND也可以称为合取(conjunction),而表达式的OR还可以叫作析取(disjunction)。
逻辑运算符也和集合的运算有相似性。
| 逻辑运算符 | 数学运算符 | 别名 | 集合运算 |
|---|---|---|---|
| AND | 积 | 合取 ∧ \wedge ∧ | 交集 ∩ \cap ∩ |
| OR | 和 | 析取 ∨ \vee ∨ | 并集 ∪ \cup ∪ |
2.2.1 简写注意点
- d = x A N D y + x A N D z + y A N D z d= x \enspace AND \enspace y +x \enspace AND \enspace z + y \enspace AND \enspace z d=xANDy+xANDz+yANDz
- d = x y + x z + y z d = xy +xz+yz d=xy+xz+yz
- d = ( x ∧ y ) ∨ ( x ∧ z ) ∨ ( y ∧ z ) d = (x \wedge y) \vee(x \wedge z) \vee(y \wedge z) d=(x∧y)∨(x∧z)∨(y∧z)
相比较来说,很明显,方式 2 更写起来方式更轻松,但它存在一个问题。在电路中,1表示真,0表示假。当x,y,z都为 1 时,在2中,d = 1 + 1 +1 = 3,这明显是错误的。
所以记住是逻辑乘,逻辑加,千万不要把方式 2 的简写形式当成数学算式运算。
2.2.2 三算律
- 结合律
(a + b) + c = a +(b + c) - 交换律
a * b = b *a - 分配率
a(b + c) = ab +ac
2.3 逻辑表达式求值
像数学表达式一样,通过逻辑运算符的优先级来分部运算。逻辑表达式的值只有两个 真(TRUE) 或 假 (FALSE)。
3 真值表
真值表中的各行对应着各参数真值所有可能的组合。表中有着对应各参数的列以及对应函数值的列。
3.1 真值表的行数
若命题有 k 个,那么, 真值表就有 2 k 2^k 2k行
3.2 真值表和文氏图
真值表与集合运算的文氏图之间存在着相似性。 真值表有几个参数,文氏图就有几个圈。并集运算就类似于OR,而交集则类似AND。
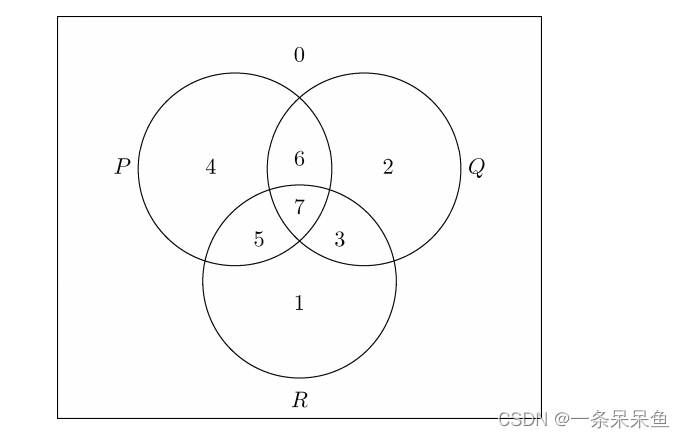
例如,具有变量p、q和r的逻辑表达式就对应涉及P、Q和R这3个集合的集合表达式。考虑对应这些集合的文氏图:
在这里,区域0对应不在P、Q、R任意一个中的元素构成的集合。区域 1 则对应着在R中但不在P或Q中的元素。一般地讲,如果考虑 3 位区域编号的二进制表示,比方说是abc,那么如果 a = 1,则表示元素在P中,如果b = 1则在Q中,而如果c = 1 则在R中。因此,编号为 ( a b c ) 2 (abc)_2 (abc)2 的区域就对应着p、q、r分别具有真值a、b、c时真值表的那行。
| 真值表 qpr | 数字 |
|---|---|
| 000 | 0 |
| 001 | 1 |
| 010 | 2 |
| 011 | 3 |
| 100 | 4 |
| 101 | 5 |
| 110 | 6 |
| 111 | 7 |
4 从真值表到逻辑表达式
我们的目的是通过真值表求出逻辑表达式,该问题是电路设计中的基础问题。表达式中的逻辑运算符可以被理解成电路的门,这样的话就存在从逻辑表达式到电子电路的直接转化。
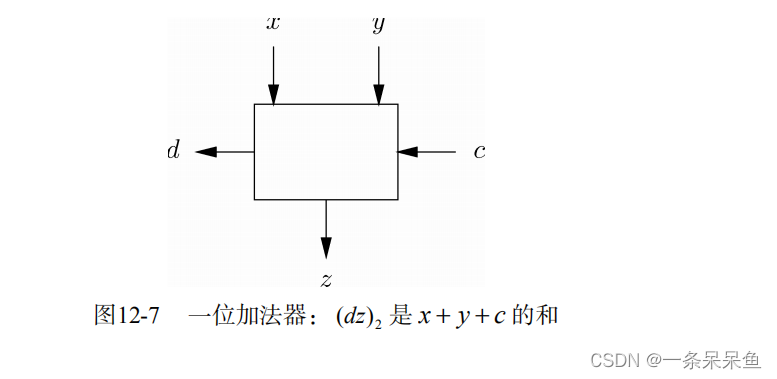 一位加法器有三个输入 x、y、c ,两个输入端 d 、z,进行二进制加法运算。
一位加法器有三个输入 x、y、c ,两个输入端 d 、z,进行二进制加法运算。
4.1 直接求逻辑表达式
从加法器的工作逻辑可以知道,它是要达到加法进位的目标,那么在 x , y , z 中如果有两个或两个以上为 1 ,那么 d 的值就一定为 1 。
d = x y + x z + y z d = xy +xz + yz d=xy+xz+yz
4.2 通过真值表求逻辑表达式
从真值表中发现某种逻辑关系,来建立逻辑表达式。这是个套路化的方法,只要有真值表,就能用此方法求出逻辑表达式。
4.2.1 真值表与析取范式
又称为积的和形式
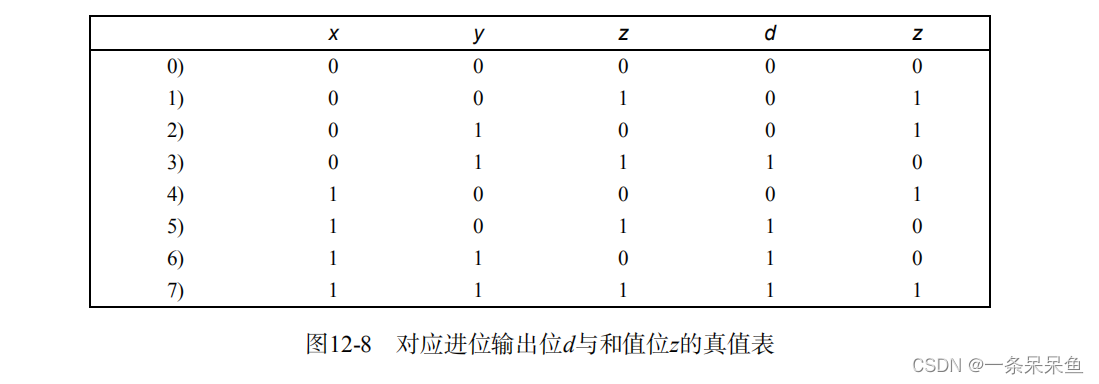
我们直接通过真值表列出所以 d=1的所有可能,就求出了逻辑表达式。
- 第3、5、6、7行d的值为1,取这几行,如果如果文字为假,则选择其否定作为文字。
d = x ‾ y z + x y ‾ z + x y z ‾ + x y z d = \overline{x}yz + x\overline{y}z + xy\overline{z}+xyz d=xyz+xyz+xyz+xyz
4.2.2 真值表与合取范式

4.3 最小项和最大项
-
最小项:n个变量的逻辑乘,即与形式,每个变量以原变量或者反变量的形式出现一次。n个变量共有 2 n 2^n 2n个最小项。用m表示,如ABC,表示为 m 0 m_0 m0。
-
最大项:n个变量的逻辑和,即或形式,每个变量以原变量或者反变量的形式出现一次。n个变量共有 2 n 2^n 2n个最大项。用M表示,如A+B+C,表示为 M 0 M_0 M0。
4.4 析取范式,合取范式
析取范式(disjunctive normal form)
合取范式(conjunction normal form)
- 文字: 命题及其否定
- 简单析取式:仅由有限个文字构成的析取式
- 简单和取式:仅由有限个文字构成的合取
- 析取范式:由有限个简单合取式构成的析取式
( p ∧ ¬ q ) ∨ ( ¬ q ∧ ¬ r ) ∨ p (p \wedge \neg q ) \vee (\neg q \wedge \neg r) \vee p (p∧¬q)∨(¬q∧¬r)∨p- 合取范式:由有限个简单析取式构成的合取式
( p ∨ q ∨ r ) ∧ ( ¬ p ∨ ¬ q ) ∧ r (p \vee q \vee r) \wedge (\neg p \vee \neg q) \wedge r (p∨q∨r)∧(¬p∨¬q)∧r
特殊情况:即是析取范式,也是合取范式 ¬ p ∧ p ∧ r , p ∨ ¬ q ∨ r \neg p \wedge p \wedge r,p \vee \neg q \vee r ¬p∧p∧r,p∨¬q∨r
4.4 运算符的完全集
完全集是指任何逻辑都可以次集元素表示。
完全集:
- AND , OR , NOT
- NAND
5 重言式
重言式(tautology)是指不管其命题变量的值如何,其值都为真的逻辑表达式。
简单的重言式
- TRUE
- p + p ‾ p+\overline{p} p+p
- ( p + q ) ≡ ( p + p ‾ q ) (p+ q) \equiv (p +\overline{p}q) (p+q)≡(p+pq)
若一个逻辑表达式中有等价,如果这个逻辑表达式是重言式,那么久可以在任何情况下用等价右边代替等价左边。
5.1 如何判断是否是重言式
列出真值表,如果次逻辑表表达式满足重言式定义,即逻辑表达式的值全为真,则是重言式。
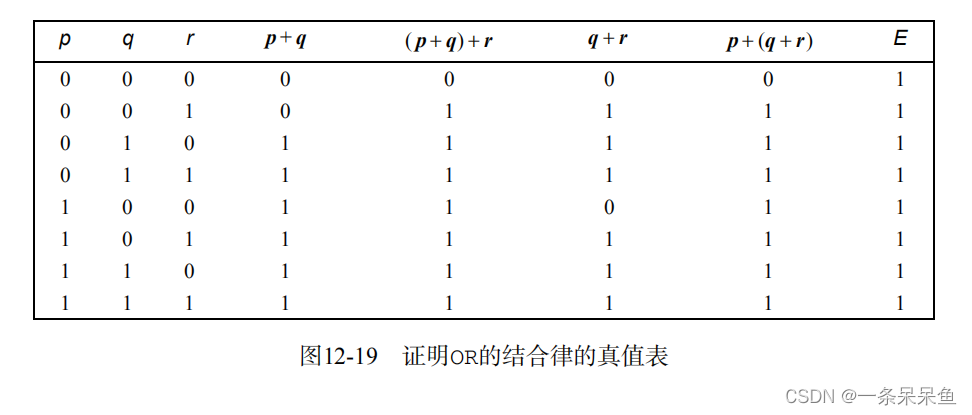
( p + q ) + r ≡ p + ( q + r ) (p +q) +r \equiv p +(q+r) (p+q)+r≡p+(q+r)
标号为E的最后一列就表示整个表达式。
5.2 重言式替换
对于一个重言式来说,因为该表达式是重言式,所以我们知道,不管为处于叶子节点处的命题变量指定什么真值,根节点的都为真(只要我们为标号为某给定变量的各个叶子节点指定相同的真值)。
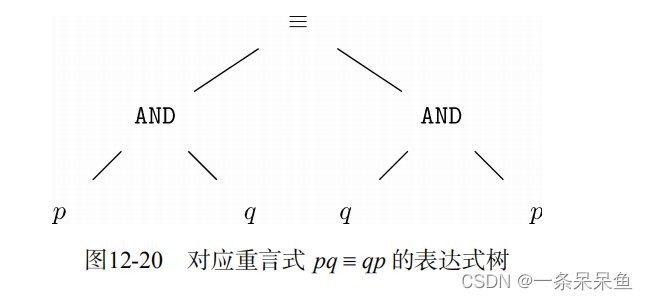
替换后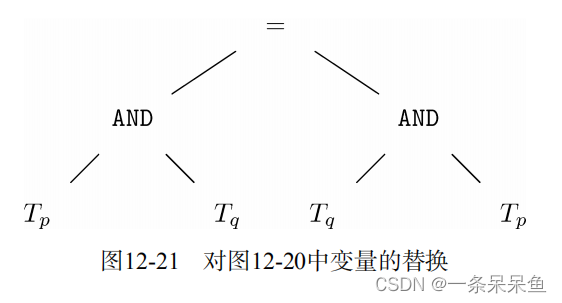
6 常用逻辑表达式代数法则
6.1 等价的法则
- 自反性: p ≡ p p \equiv p p≡p
- 交换律: ( p ≡ q ) ≡ ( q ≡ p ) (p \equiv q) \equiv (q \equiv p) (p≡q)≡(q≡p)
- 传递性: ( ( p ≡ q ) A N D ( q ≡ r ) ) → ( p ≡ r ) ((p \equiv q) AND (q \equiv r)) \to (p \equiv r) ((p≡q)AND(q≡r))→(p≡r)
- 否定的等价: ( p ≡ q ) ≡ ( p ‾ ≡ q ‾ ) (p \equiv q) \equiv (\overline{p} \equiv \overline{q}) (p≡q)≡(p≡q)
6.2 类似算数的法则
- AND 交换律: p q ≡ q p pq \equiv qp pq≡qp
- AND 结合律: p ( q r ) ≡ ( p q ) r p(qr) \equiv (pq)r p(qr)≡(pq)r
- OR 交换律: ( q + p ) ≡ ( p + q ) (q +p) \equiv (p +q) (q+p)≡(p+q)
- OR 结合律: ( p + ( q + r ) ) ≡ ( ( p + q ) + r ) (p +(q +r)) \equiv ((p +q)+r) (p+(q+r))≡((p+q)+r)
- AND对OR的分配律: p ( q + r ) ≡ ( p q + p r ) p(q +r) \equiv (pq +pr) p(q+r)≡(pq+pr)
- 双重否定抵消 : ( N O T N O T p ) ≡ p (NOT \enspace NOT \enspace p) \equiv p (NOTNOTp)≡p
6.3 AND 和 OR 与加和乘的区别
- OR 对 AND 的分配律: ( p + q r ) ≡ ( ( p + q ) ( p + r ) ) (p +qr) \equiv ((p+q)(p+r)) (p+qr)≡((p+q)(p+r))
- 等价右边可以化为 p p + p q + p r + q r pp + pq +pr +qr pp+pq+pr+qr , p q , p r pq,pr pq,pr永远和 p p p的真假一样,又有AND的幂等性,所以可证。
- 1是OR的零元: ( 1 O R p ) ≡ 1 (1 \enspace OR \enspace p) \equiv 1 (1ORp)≡1
- AND的幂等性: p p ≡ p pp \equiv p pp≡p
- OR的幂等性: p + p ≡ p p +p \equiv p p+p≡p
- 吸收律:这一法则有两个版本,取决于我们想消除的是多余的积还是多余的和。
- ( p + p q ) ≡ p (p +pq) \equiv p (p+pq)≡p
- p ( p + q ) ≡ p p(p+q) \equiv p p(p+q)≡p
- 否定的消除
- p ( p ‾ + q ) ≡ p q p(\overline{p} +q) \equiv pq p(p+q)≡pq
- p + p ‾ q ≡ p + q p + \overline{p}q \equiv p +q p+pq≡p+q
6.4 德摩根律
- N O T ( p q ) ≡ p ‾ + q ‾ NOT(pq) \equiv \overline{p} + \overline{q} NOT(pq)≡p+q
- N O T ( p + q ) ≡ p ‾ q ‾ NOT(p +q) \equiv \overline{p}\overline{q} NOT(p+q)≡pq
6.5涉及蕴涵的法则
- ( p → q ) ≡ ( p ‾ + q ) (p \to q) \equiv (\overline{p}+q) (p→q)≡(p+q)
- ( p → q ) A N D ( q → p ) ≡ ( p ≡ q ) (p \to q) AND(q \to p) \equiv(p \equiv q) (p→q)AND(q→p)≡(p≡q)
- 蕴涵的传递性: ( ( p → q ) A N D ( q → r ) ) → ( p → r ) ((p \to q)AND (q \to r)) \to (p \to r) ((p→q)AND(q→r))→(p→r)
